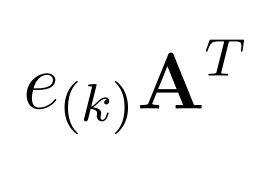
Table of Contents
Inequalities
(Cauchy-Schwarz)
Let \( u \) and \( v \) be arbitrary vectors in an inner product space over the scalar field \( \mathbb R \) or \( \mathbb C \).
Then,
$$
|x^\top y| \le \lVert x \rVert \lVert y \rVert
$$
with equality holding if and only if \( u \) and \( v \) are linearly dependent.
Proof
Available on the Cauchy–Schwarz inequality Wikipedia page.
Let \( A\in\mathbb R^{m\times n} \) be a given full-rank matrix. Then, for any \( x\in\mathbb R^n \),
$$
\sigma_{\min}(A) \lVert x \rVert \le \lVert Ax \rVert
$$
Derivatives
- \( \nabla_{\mathbf x} \mathbf a = \mathbf 0 \)
- \( \nabla_{\mathbf x} \mathbf a^\top\mathbf x = \mathbf a \)
- \( \nabla_{\mathbf X} \mathbf a^\top\mathbf X\mathbf b = \mathbf a\mathbf b^\top \)
- \( \nabla_{\mathbf X} \mathbf a^\top\mathbf X^\top\mathbf b = \mathbf b\mathbf a^\top \)
- \( \nabla_{\mathbf x} (\mathbf x^\top\mathbf A\mathbf x + \mathbf b^\top\mathbf x) = (\mathbf A + \mathbf A^\top)\mathbf x + \mathbf b \)
- \( \nabla_{\mathbf x} || \mathbf x - \mathbf a ||_2 = \frac{ \mathbf x - \mathbf a }{ || \mathbf x - \mathbf a ||_2 } \)
- \( \nabla_{\mathbf x} ||\mathbf x ||_2^2 = 2\mathbf x \)
- Let \(g(x) = f(Ax + b) \), then \( \nabla g(x) = A^\top \nabla f(Ax + b) \)
Rows and Columns
Let \( \mathbf{A}\in\mathbb{R}^{m\times n} \), \(\mathbf{b}\in\mathbb{R}^{m\times 1} \) and \( \mathbf{c}\in\mathbb{R}^{n\times 1} \). We denote by \( \ a_{ij} \) the \( (i,j) \)-th component of \( \mathbf{A} \), by \( \mathbf{a}^{(j)} \) its \( j \)-th column and by \( \mathbf{a}_{(i)} \) its \( i \)-th row. Vector \( \mathbf{e}^{(j)} \) (resp. \( \mathbf{e}_{(j)} \)) denote the \( j \)-th column (resp. the \(i\)-th row) of the identity matrix.- \( \mathbf{e}_{(k)}^\top = \mathbf{e}^{(k)} \)
- \( \mathbf{e} = \sum_{k=1}^K \mathbf{e}^{(k)} \quad ; \quad \mathbf{e}^\top = \sum_{k=1}^K \mathbf{e}_{(k)} \)
- \( \mathbf{A}\mathbf{e}^{(j)} = \mathbf{a}^{(j)} \) with \( j\in [n] \)
- \( \mathbf{A}^\top\mathbf{e}^{(i)} = \mathbf{a}_{(i)}^\top \) with \( i\in[m] \)
- \( \mathbf{e}_{(i)}\mathbf{A} = \mathbf{a}_{(i)} \) with \( i\in[m] \)
- \( \mathbf{e}_{(j)}\mathbf{A}^\top = {\mathbf{a}^{(j)}}^\top \) with \( j\in[n] \)
- \( \mathbf{e}_{(i)}\mathbf{A}\mathbf{e}^{(j)} = a_{ij} \) with \( i\in[m], j\in[n] \)
- \( \mathbf{e}^\top\mathbf{A} = \sum_{i=1}^m \mathbf{a}_{(i)} \)
- \( \mathbf{A}\mathbf{e} = \sum_{j=1}^n \mathbf{a}^{(j)} \)
- \( \mathbf{e}^\top\mathbf{A}\mathbf{c} = \sum_{i=1}^m \mathbf{a}_{(i)}\mathbf{c} \)
- \( \mathbf{e}^\top\mathbf{A}^\top\mathbf{b} = \sum_{j=1}^n \mathbf{b}^\top\mathbf{a}^{(j)} \)
- \( \mathbf{b}^\top\mathbf{e}^{(i)} = \mathbf{e}_{(i)}\mathbf{b} = b_i \) with \( i\in[m] \)
- \( \mathbf{A}\mathbf{c} = \begin{pmatrix} \mathbf{a}_{(1)}\mathbf{c} \\ \vdots \\ \mathbf{a}_{(m)}\mathbf{c} \end{pmatrix} \) or \( [\mathbf{Ac}]_{(i)} = \mathbf{a}_{(i)}\mathbf{c} \)
- \( \mathbf{A}^\top\mathbf{b} = \begin{pmatrix} \mathbf{b}^\top\mathbf{a}^{(1)} \\ \vdots \\ \mathbf{b}^\top\mathbf{a}^{(n)} \end{pmatrix} \) or \( [\mathbf{A}^\top\mathbf{b}]_{(j)} = \mathbf{b}^\top\mathbf{a}^{(j)} \)
- \( \mathbf a^\top\mathbf a = \textrm{Tr}(\mathbf a\mathbf a^\top) \)