Table of Contents
A Two-stage Robust Approach for Minimizing the Weighted Number of Tardy Jobs with Objective Uncertainty
Reading instances
The CSV file
All our results can be found in the CSV file results.csv
which contains the following rows and columns.
all_results = read.csv("results.csv", na.strings = "")Here, columns have the following inerpretation:
- instance: instance file name ;
- problem: 1 if the row relates to problem \((\mathcal P)\), 2 if it relates to problem \((\widetilde{\mathcal P})\) ;
- approach: the approach used for solving the instance,
- For problem \((\mathcal P)\), possible values are “colgen, kadapt-a, kadapt-b” (in the paper: ColGen1, KAdapt1-a, KAdapt1-b) ;
- For problem \((\widetilde{\mathcal P})\), possible values are “colgen, colgen-ext, kadapt-a” (in the paper: ColGen2, ColGen3, KAdapt2)
- n_jobs: the number of jobs ;
- gamma: the value for \(\Gamma\) ;
- k: when using a \(K\)-adaptability approach, the value for \(K\) ;
- cpu: the CPU time needed to sovle the instance (3600 if the time-limit is reached) ;
- objective: the best objective value found (i.e., optimal if cpu < 3600) ;
- n_active_col: when the column generation approach is used, the number of active columns ;
- quality: the solution quality,
- When column generation is used, possible values are “Optimal, TimeLimitFeasible, TimeLimitInfeasible” ;
- When \(K\)-adaptability is used, possible values are “Optimal, Time Lim, Mem Lim”.
- gap: the remaining optimality gap after 1 hour of computation ;
- rule_for_branching: when the column generation approach is used, the variable selection rule which were used (possible values: “default, strong_branching”, i.e., most infeasible).
all_results[all_results$cpu > 3600, ] = 3600problem1 = all_results[all_results$problem == 1,]
problem2 = all_results[all_results$problem == 2,]create_approach = function(problem, approach) {
result = problem[problem$approach == approach & problem$rule_for_branching == 'default',]
result = result[,!names(result) %in% c("approach", "problem", "rule_for_branching", "quality", "n_active_col")]
rownames(result) = NULL
return (result)
}colgen1 = create_approach(problem1, 'colgen')
kadapt1_a = create_approach(problem1, 'kadapt-a')
kadapt1_b = create_approach(problem1, 'kadapt-b')colgen2 = create_approach(problem2, 'colgen')
colgen3 = create_approach(problem2, 'colgen-ext')
kadapt2_a = create_approach(problem2, 'kadapt-a')
kadapt2_b = create_approach(problem2, 'kadapt-b')Estimating \(K^*\) (finding \(\widehat{K}^*\))
estimate_k_star = function(exact_method, k_adaptability) {
# We first merge the exact method with the K-adaptability approach
k_stars = merge(exact_method, k_adaptability, by = c("instance", "gamma"), all.y = TRUE)
# We only keep those values of K which trigger the stopping condition
k_stars = k_stars[
# - (P_K)^* <= (P)^*, t(P) <= T, t(P_K) <= T
(k_stars$objective.y <= k_stars$objective.x + 1e-3 & k_stars$time.x < 3600 & k_stars$time.y < 3600)
|
# - (P_K)^* <= (P)^*, t(P) > T, t(P_K) <= T
(k_stars$objective.y <= k_stars$objective.x + 1e-3 & k_stars$time.x >= 3600 & k_stars$time.y < 3600)
|
# - t(P) <= P, t(P_K) > T
(k_stars$time.x < 3600 & k_stars$time.y >= 3600)
|
# - t(P) > T, t(P_K) > T
(k_stars$time.x >= 3600 & k_stars$time.y >= 3600)
,
c("instance", "gamma", "k.y")
]
# We rename k.y as k
colnames(k_stars)[3] = "k"
# Keep only the first (instance, gamma, k) which triggered the stopping criteria
k_stars = k_stars[order(k_stars$instance, k_stars$gamma, k_stars$k),]
k_stars = k_stars[!duplicated(( k_stars[,c("instance", "gamma")] )),]
return (k_stars)
}k_star1_a = estimate_k_star(colgen1, kadapt1_a)
k_star1_b = estimate_k_star(colgen1, kadapt1_b)
k_star2_a = estimate_k_star(colgen2, kadapt2_a)
k_star2_b = estimate_k_star(colgen2, kadapt2_b)The \(\widehat{K}^*\)-adaptability
create_optimal_kadapt = function(k_adaptability, k_star) {
opt_kadapt = merge(k_adaptability, k_star, by = c("instance", "gamma", "k"))
return(opt_kadapt)
}opt_kadapt1_a = create_optimal_kadapt(kadapt1_a, k_star1_a)
opt_kadapt1_b = create_optimal_kadapt(kadapt1_b, k_star1_b)
opt_kadapt2_a = create_optimal_kadapt(kadapt2_a, k_star2_a)
opt_kadapt2_b = create_optimal_kadapt(kadapt2_b, k_star2_b)Analysis
Computational times
compute_mean_times_by_group = function(data) {
data = data[data$time < 3600,]
mean_times = aggregate(data$time, list(data$n_jobs, data$gamma), mean)
colnames(mean_times) = c("n_jobs", "gamma", "time")
mean_times = mean_times[order(mean_times$n_jobs, mean_times$gamma),]
rownames(mean_times) = NULL
return(mean_times)
}mean_times_colgen1 = compute_mean_times_by_group(colgen1)
mean_times_kadapt1_a = compute_mean_times_by_group(opt_kadapt1_a)
mean_times_kadapt1_b = compute_mean_times_by_group(opt_kadapt1_b)
mean_times_colgen2 = compute_mean_times_by_group(colgen2)
mean_times_colgen3 = compute_mean_times_by_group(colgen3)
mean_times_kadapt2_a = compute_mean_times_by_group(opt_kadapt2_a)
mean_times_kadapt2_b = compute_mean_times_by_group(opt_kadapt2_b)compute_number_unsolved_by_group = function(data) {
unsolved = aggregate(data$time >= 3600, list(data$n_jobs, data$gamma), sum)
colnames(unsolved) = c("n_jobs", "gamma", "unsolved")
total = aggregate(data$instance, list(data$n_jobs, data$gamma), length)
colnames(total) = c("n_jobs", "gamma", "total")
unsolved$unsolved = unsolved$unsolved / total$total * 100
unsolved = unsolved[order(unsolved$n_jobs, unsolved$gamma),]
rownames(unsolved) = NULL
return(unsolved)
}unsolved_colgen1 = compute_number_unsolved_by_group(colgen1)
unsolved_kadapt1_a = compute_number_unsolved_by_group(opt_kadapt1_a)
unsolved_kadapt1_b = compute_number_unsolved_by_group(opt_kadapt1_b)
unsolved_colgen2 = compute_number_unsolved_by_group(colgen2)
unsolved_colgen3 = compute_number_unsolved_by_group(colgen3)
unsolved_kadapt2_a = compute_number_unsolved_by_group(opt_kadapt2_a)
unsolved_kadapt2_b = compute_number_unsolved_by_group(opt_kadapt2_b)compute_fastest_approach = function(t_colgen, t_kadapta, t_kadaptb) {
fastest = merge(t_colgen, t_kadapta, by = c("instance", "gamma"))
fastest = fastest[,c("instance", "gamma", "n_jobs.x", "time.x", "time.y")]
colnames(fastest) = c("instance", "gamma", "n_jobs", "time_colgen", "time_kadapt_a")
fastest = merge(fastest, t_kadaptb, by = c("instance", "gamma"))
fastest = fastest[,c("instance", "gamma", "n_jobs.x", "time_colgen", "time_kadapt_a", "time")]
colnames(fastest)[3] = "n_jobs"
colnames(fastest)[6] = "time_kadapt_b"
fastest$best_time = apply(fastest[,c("time_colgen", "time_kadapt_a", "time_kadapt_b")], 1, FUN = min)
fastest$best_is_colgen = fastest$time_colgen == fastest$best_time
fastest$best_is_kadapt_a = fastest$time_kadapt_a == fastest$best_time
fastest$best_is_kadapt_b = fastest$time_kadapt_b == fastest$best_time
return(fastest)
}
fastest1 = compute_fastest_approach(colgen1, opt_kadapt1_a, opt_kadapt1_b)
fastest2 = compute_fastest_approach(colgen2, opt_kadapt2_a, opt_kadapt2_b)compute_fastest_approach_by_group = function(fastest) {
fastest = aggregate(fastest[,c("best_is_colgen", "best_is_kadapt_a", "best_is_kadapt_b")], by = list(fastest$n_jobs, fastest$gamma), sum)
fastest[,3:5] = fastest[,3:5] / rowSums(fastest[,3:5]) * 100
colnames(fastest) = c("n_jobs", "gamma", "best_is_colgen", "best_is_kadapt_a", "best_is_kadapt_b")
fastest = fastest[order(fastest$n_jobs, fastest$gamma),]
rownames(fastest) = NULL
return (fastest);
}fastest_by_group1 = compute_fastest_approach_by_group(fastest1)
fastest_by_group2 = compute_fastest_approach_by_group(fastest2)For problem \(({\mathcal P})\)
Table41 = cbind(unsolved_kadapt1_a,
unsolved_kadapt1_b$unsolved,
unsolved_colgen1$unsolved,
mean_times_kadapt1_a$time,
mean_times_kadapt1_b$time,
mean_times_colgen1$time,
fastest_by_group1$best_is_kadapt_a,
fastest_by_group1$best_is_kadapt_b,
fastest_by_group1$best_is_colgen
)|
Unsolved
|
Time
|
Fastest
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(&#124;\mathcal J&#124;\) | \(\Gamma\) | KAdapt1-a | KAdapt1-b | ColGen1 | KAdapt1-a | KAdapt1-b | ColGen1 | KAdapt1-a | KAdapt1-b | ColGen1 |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 10 | 90 | 0 |
| 5 | 2 | 0 | 1 | 0 | 0 | 0 | 2 | 4 | 96 | 0 |
| 5 | 3 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 99 | 0 |
| 10 | 1 | 6 | 12 | 0 | 85 | 59 | 13 | 11 | 76 | 12 |
| 10 | 2 | 11 | 24 | 0 | 49 | 30 | 15 | 18 | 64 | 19 |
| 10 | 3 | 5 | 10 | 0 | 17 | 1 | 11 | 5 | 85 | 10 |
| 10 | 4 | 1 | 2 | 0 | 0 | 1 | 8 | 1 | 96 | 2 |
| 10 | 5 | 1 | 2 | 0 | 7 | 0 | 7 | 1 | 96 | 2 |
| 10 | 6 | 0 | 0 | 0 | 0 | 0 | 7 | 1 | 99 | 0 |
| 10 | 7 | 0 | 0 | 0 | 0 | 0 | 7 | 1 | 99 | 0 |
| 15 | 1 | 35 | 28 | 0 | 443 | 207 | 43 | 8 | 50 | 42 |
| 15 | 2 | 57 | 69 | 0 | 452 | 27 | 69 | 4 | 28 | 69 |
| 15 | 3 | 46 | 49 | 0 | 16 | 1 | 64 | 1 | 50 | 49 |
| 15 | 4 | 29 | 29 | 0 | 55 | 0 | 47 | 4 | 68 | 29 |
| 15 | 5 | 12 | 12 | 0 | 0 | 0 | 29 | 6 | 81 | 12 |
| 15 | 6 | 10 | 10 | 0 | 0 | 0 | 23 | 2 | 88 | 10 |
| 15 | 7 | 2 | 2 | 0 | 0 | 0 | 21 | 4 | 94 | 2 |
| 15 | 8 | 0 | 0 | 0 | 0 | 0 | 17 | 4 | 96 | 0 |
| 15 | 9 | 0 | 0 | 0 | 0 | 0 | 16 | 1 | 99 | 0 |
| 15 | 10 | 0 | 0 | 0 | 0 | 0 | 16 | 1 | 99 | 0 |
| 20 | 1 | 66 | 45 | 0 | 693 | 184 | 118 | 2 | 44 | 54 |
| 20 | 2 | 88 | 86 | 0 | 171 | 39 | 190 | 4 | 12 | 84 |
| 20 | 3 | 86 | 91 | 0 | 306 | 42 | 273 | 5 | 6 | 89 |
| 20 | 4 | 71 | 76 | 0 | 132 | 20 | 332 | 6 | 19 | 75 |
| 20 | 5 | 55 | 56 | 0 | 20 | 1 | 346 | 5 | 39 | 56 |
| 20 | 6 | 35 | 35 | 0 | 0 | 0 | 269 | 16 | 49 | 35 |
| 20 | 7 | 20 | 20 | 0 | 0 | 0 | 188 | 20 | 60 | 20 |
| 20 | 8 | 5 | 5 | 0 | 0 | 0 | 127 | 31 | 64 | 5 |
| 20 | 9 | 0 | 0 | 0 | 0 | 0 | 67 | 34 | 66 | 0 |
| 20 | 10 | 0 | 0 | 0 | 0 | 0 | 46 | 28 | 72 | 0 |
| 25 | 1 | 82 | 59 | 9 | 384 | 345 | 375 | 8 | 30 | 62 |
| 25 | 2 | 95 | 95 | 12 | 78 | 45 | 623 | 11 | 9 | 79 |
| 25 | 3 | 91 | 92 | 16 | 5 | 0 | 629 | 15 | 16 | 69 |
| 25 | 4 | 78 | 78 | 19 | 0 | 0 | 613 | 18 | 25 | 56 |
| 25 | 5 | 66 | 66 | 21 | 0 | 1 | 538 | 25 | 29 | 46 |
| 25 | 6 | 57 | 57 | 20 | 0 | 1 | 534 | 29 | 29 | 41 |
| 25 | 7 | 39 | 39 | 18 | 0 | 0 | 442 | 33 | 38 | 30 |
| 25 | 8 | 31 | 31 | 12 | 0 | 1 | 442 | 38 | 37 | 26 |
| 25 | 9 | 15 | 15 | 10 | 0 | 1 | 426 | 50 | 37 | 13 |
| 25 | 10 | 6 | 6 | 5 | 0 | 2 | 286 | 59 | 35 | 6 |
Table41_mean_unsolved_by_group = aggregate(Table41[,c(3:5)], by = list(Table41$n_jobs), mean)
colnames(Table41_mean_unsolved_by_group ) = c("n_jobs", "unsolved_k1_a", "unsolved_k1_b", "unsolved_c1")
Table41_mean_times_by_group = aggregate(Table41[,c(6:8)], by = list(Table41$n_jobs), mean)
colnames(Table41_mean_times_by_group) = c("n_jobs", "time_k1_a", "time_k1_b", "time_c1")
Table41_fastest_by_group = aggregate(Table41[,c(9:11)], by = list(Table41$n_jobs), mean)
colnames(Table41_fastest_by_group) = c("n_jobs", "fastest_k1_a", "fastest_k1_b", "fastest_c1")
Table41_summary = merge(Table41_mean_unsolved_by_group , Table41_mean_times_by_group, by = c("n_jobs"))
Table41_summary = merge(Table41_summary, Table41_fastest_by_group, by = c("n_jobs"))|
Unsolved
|
Time
|
Fastest
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| \(&#124;\mathcal J&#124;\) | KAdapt1-a | KAdapt1-b | ColGen1 | KAdapt1-a | KAdapt1-b | ColGen1 | KAdapt1-a | KAdapt1-b | ColGen1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 2 | 5 | 95 | 0 |
| 10 | 4 | 7 | 0 | 22 | 13 | 10 | 6 | 88 | 7 |
| 15 | 19 | 20 | 0 | 97 | 24 | 35 | 3 | 75 | 21 |
| 20 | 43 | 42 | 0 | 132 | 29 | 196 | 15 | 43 | 42 |
| 25 | 56 | 54 | 14 | 47 | 40 | 491 | 29 | 29 | 43 |
For problem \((\widetilde{\mathcal P})\)
Table44 = cbind(unsolved_kadapt2_a,
unsolved_kadapt2_b$unsolved,
unsolved_colgen2$unsolved,
mean_times_kadapt2_a$time,
mean_times_kadapt2_b$time,
mean_times_colgen2$time,
fastest_by_group2$best_is_kadapt_a,
fastest_by_group2$best_is_kadapt_b,
fastest_by_group2$best_is_colgen
)|
Unsolved
|
Time
|
Fastest
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(&#124;\mathcal J&#124;\) | \(\Gamma\) | KAdapt1-a | KAdapt1-b | ColGen1 | KAdapt1-a | KAdapt1-b | ColGen1 | KAdapt1-a | KAdapt1-b | ColGen1 |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 12 | 87 | 1 |
| 5 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | 14 | 86 | 0 |
| 5 | 3 | 0 | 0 | 0 | 0 | 0 | 1 | 7 | 93 | 0 |
| 10 | 1 | 0 | 11 | 0 | 14 | 27 | 28 | 22 | 72 | 5 |
| 10 | 2 | 1 | 22 | 0 | 22 | 18 | 24 | 28 | 59 | 14 |
| 10 | 3 | 1 | 9 | 0 | 9 | 4 | 11 | 16 | 78 | 6 |
| 10 | 4 | 0 | 2 | 0 | 43 | 2 | 8 | 6 | 91 | 2 |
| 10 | 5 | 0 | 1 | 0 | 37 | 40 | 4 | 12 | 86 | 1 |
| 10 | 6 | 0 | 0 | 0 | 0 | 0 | 3 | 6 | 94 | 0 |
| 10 | 7 | 0 | 0 | 0 | 0 | 0 | 3 | 8 | 92 | 0 |
| 15 | 1 | 11 | 18 | 8 | 191 | 118 | 243 | 14 | 61 | 25 |
| 15 | 2 | 36 | 55 | 16 | 212 | 280 | 219 | 25 | 27 | 48 |
| 15 | 3 | 25 | 38 | 12 | 154 | 0 | 158 | 19 | 46 | 35 |
| 15 | 4 | 19 | 26 | 8 | 131 | 0 | 169 | 21 | 56 | 23 |
| 15 | 5 | 9 | 10 | 4 | 24 | 0 | 77 | 18 | 74 | 9 |
| 15 | 6 | 5 | 6 | 4 | 8 | 0 | 47 | 20 | 76 | 5 |
| 15 | 7 | 2 | 2 | 2 | 0 | 0 | 61 | 23 | 74 | 2 |
| 15 | 8 | 0 | 0 | 0 | 0 | 0 | 50 | 19 | 81 | 0 |
| 15 | 9 | 0 | 0 | 0 | 0 | 0 | 15 | 12 | 88 | 0 |
Table44_mean_unsolved_by_group = aggregate(Table44[,c(3:5)], by = list(Table44$n_jobs), mean)
colnames(Table44_mean_unsolved_by_group) = c("n_jobs", "unsolved_k2_a", "unsolved_k2_b", "unsolved_c2")
Table44_mean_times_by_group = aggregate(Table44[,c(6:8)], by = list(Table44$n_jobs), mean)
colnames(Table44_mean_times_by_group) = c("n_jobs", "time_k2_a", "time_k2_b", "time_c2")
Table44_fastest_by_group = aggregate(Table44[,c(9:11)], by = list(Table44$n_jobs), mean)
colnames(Table44_fastest_by_group) = c("n_jobs", "fastest_k2_a", "fastest_k2_b", "fastest_c2")
Table44_summary = merge(Table44_mean_unsolved_by_group, Table44_mean_times_by_group, by = c("n_jobs"))
Table44_summary = merge(Table44_summary, Table44_fastest_by_group, by = c("n_jobs"))|
Unsolved
|
Time
|
Fastest
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| \(&#124;\mathcal J&#124;\) | KAdapt1-a | KAdapt1-b | ColGen1 | KAdapt1-a | KAdapt1-b | ColGen1 | KAdapt1-a | KAdapt1-b | ColGen1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 11 | 88 | 0 |
| 10 | 0 | 7 | 0 | 18 | 13 | 12 | 14 | 82 | 4 |
| 15 | 12 | 17 | 6 | 80 | 44 | 115 | 19 | 65 | 16 |
Performance profiles
plot_performance_profile = function(fastest, title = "Performance profile", prefix.output.file = "") {
perf_colgen = fastest$time_colgen / fastest$best_time
perf_kadapt_a = fastest$time_kadapt_a / fastest$best_time
perf_kadapt_b = fastest$time_kadapt_b / fastest$best_time
max_perf = max( max(perf_colgen), max(perf_kadapt_a), max(perf_kadapt_b) ) + 1
perf_colgen[fastest$time_colgen >= 3600] = max_perf
perf_kadapt_a[fastest$time_kadapt_a >= 3600] = max_perf
perf_kadapt_b[fastest$time_kadapt_b >= 3600] = max_perf
perf_profile_colgen = ecdf(perf_colgen)
perf_profile_kadapt_a = ecdf(perf_kadapt_a)
perf_profile_kadapt_b = ecdf(perf_kadapt_b)
if (prefix.output.file != "") {
x.axis = seq(from = 1, to = 10, by = .05)
save.to.file = function (ecdf_function, method) {
y.axis = ecdf_function(x.axis)
write.csv(data.frame(x = x.axis, y = y.axis), paste0(prefix.output.file, ".", method, ".", "generated.csv"), row.names = FALSE)
}
save.to.file(perf_profile_colgen, "colgen")
save.to.file(perf_profile_kadapt_a, "kadapt_a")
save.to.file(perf_profile_kadapt_b, "kadapt_b")
all_files = dir()
files = all_files[str_detect(all_files, prefix.output.file)]
zip(zipfile = paste0(prefix.output.file, ".generated.zip"), files = files)
}
xlim = c(1, 10)
ylim = c(0, 1)
plot(perf_profile_colgen, col = "blue", xlim = xlim, ylim = ylim, lty = "solid", cex = 0, main = title)
lines(perf_profile_kadapt_a, col = "green", xlim = xlim, ylim = ylim, lty = "dotted", cex = 0)
lines(perf_profile_kadapt_b, col = "red", xlim = xlim, ylim = ylim, lty = "dashed", cex = 0)
legend(
6, .5, legend = c("ColGen", "KAdapt-a", "KAdapt-b"), col = c("blue", "green", "red"), lty = c("solid", "dotted", "dashed")
)
}For problem \((\mathcal P)\)
plot_performance_profile(fastest1, title = "Over all instances", prefix.output.file = "problem1.all")
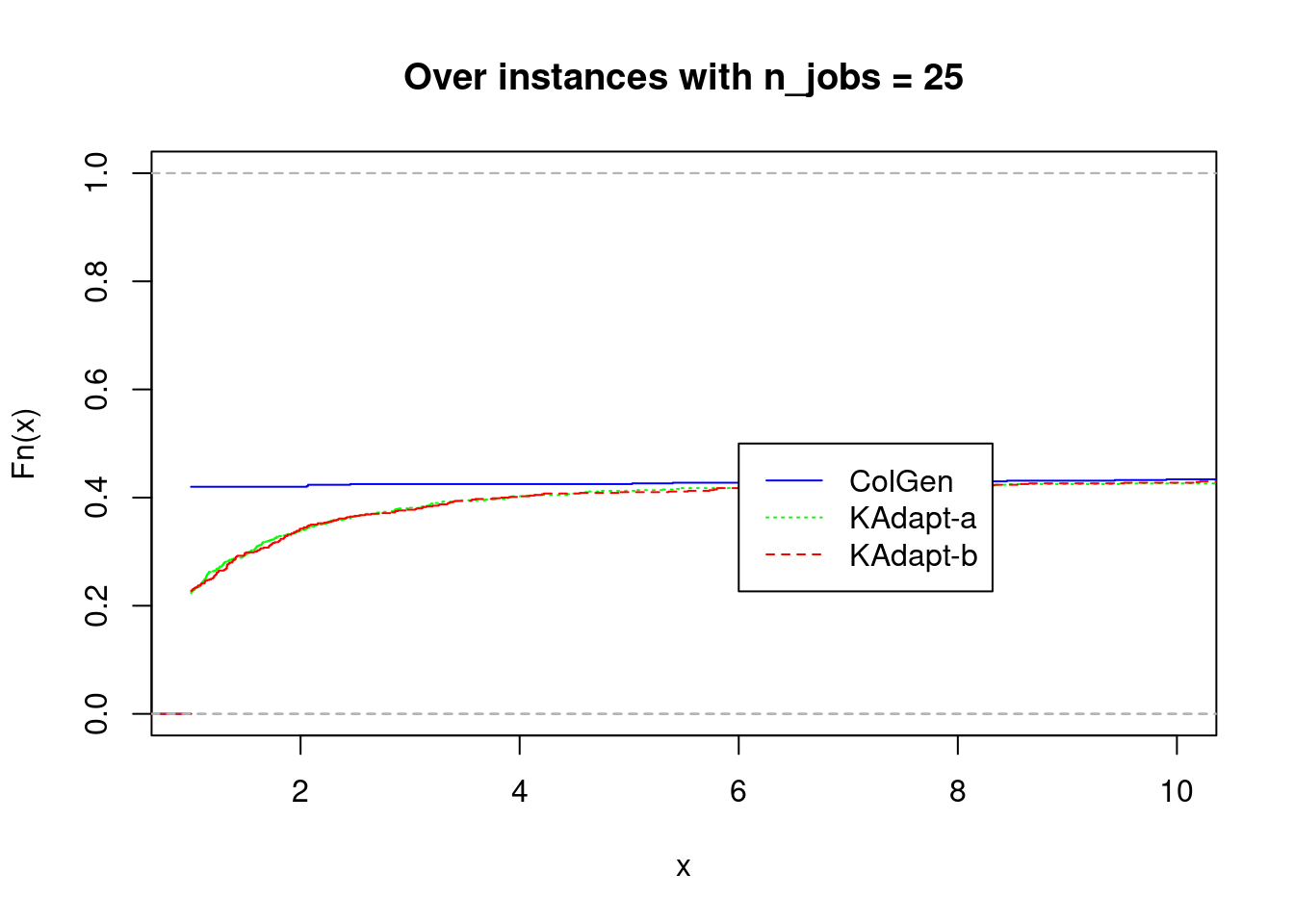
plot_performance_profile(fastest1[fastest1$n_jobs == 25,], title = "Over instances with n_jobs = 25", prefix.output.file = "problem1.25jobs")
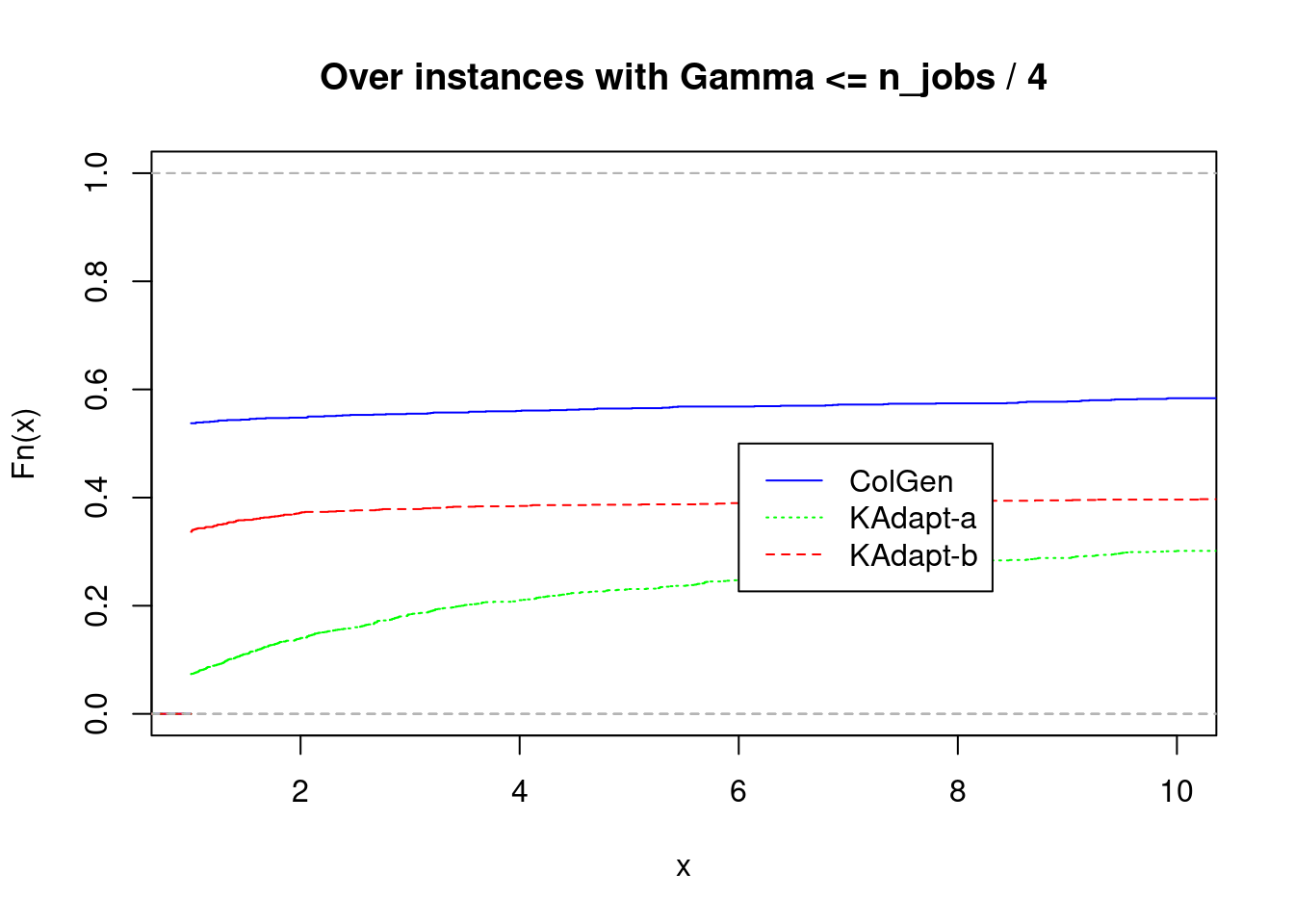
plot_performance_profile(fastest1[fastest1$gamma <= fastest1$n_jobs / 4,], title = "Over instances with Gamma <= n_jobs / 4", prefix.output.file = "problem1.hard")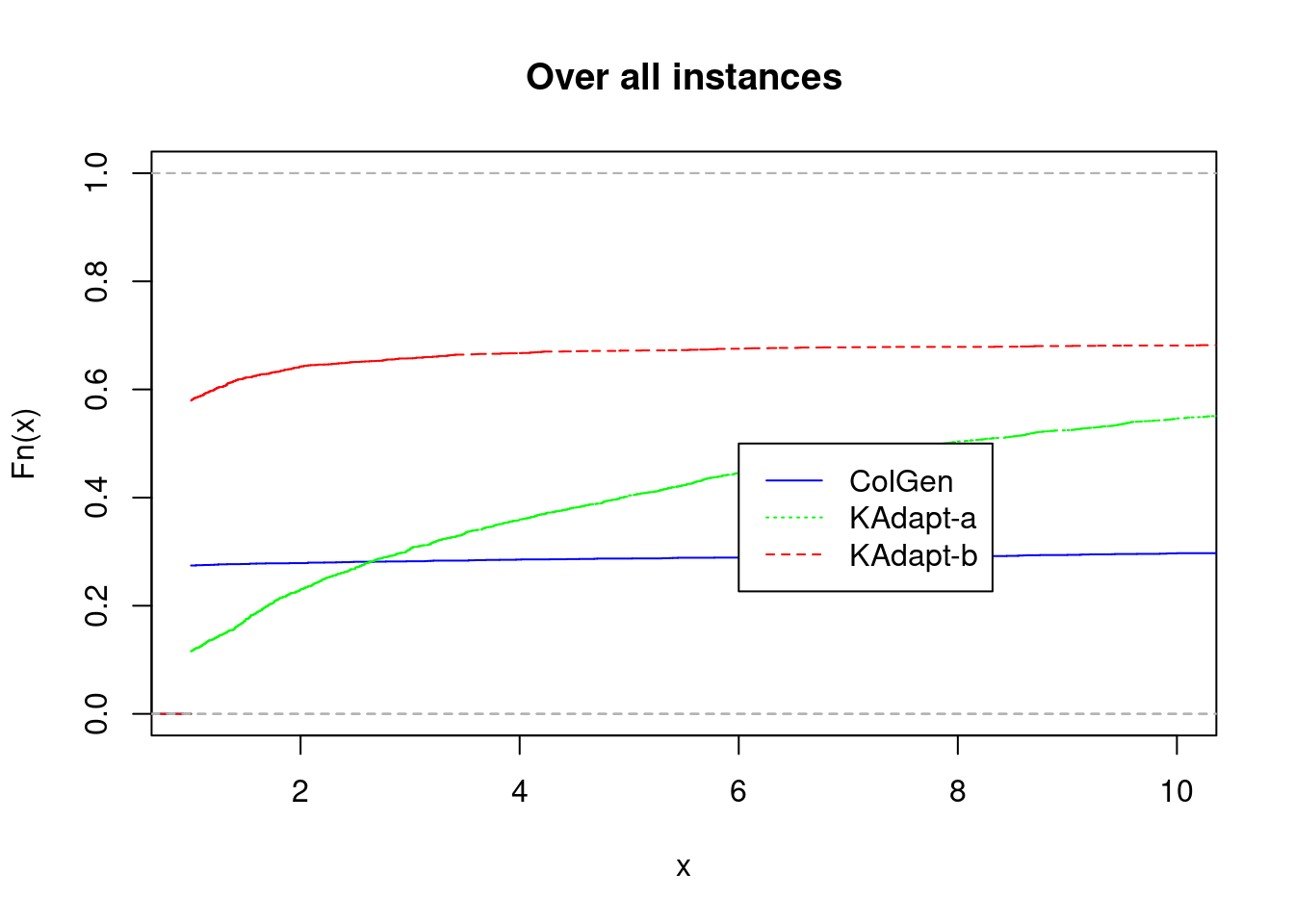
For problem \((\widetilde{\mathcal P})\)
plot_performance_profile(fastest2, title = "Over all instances")
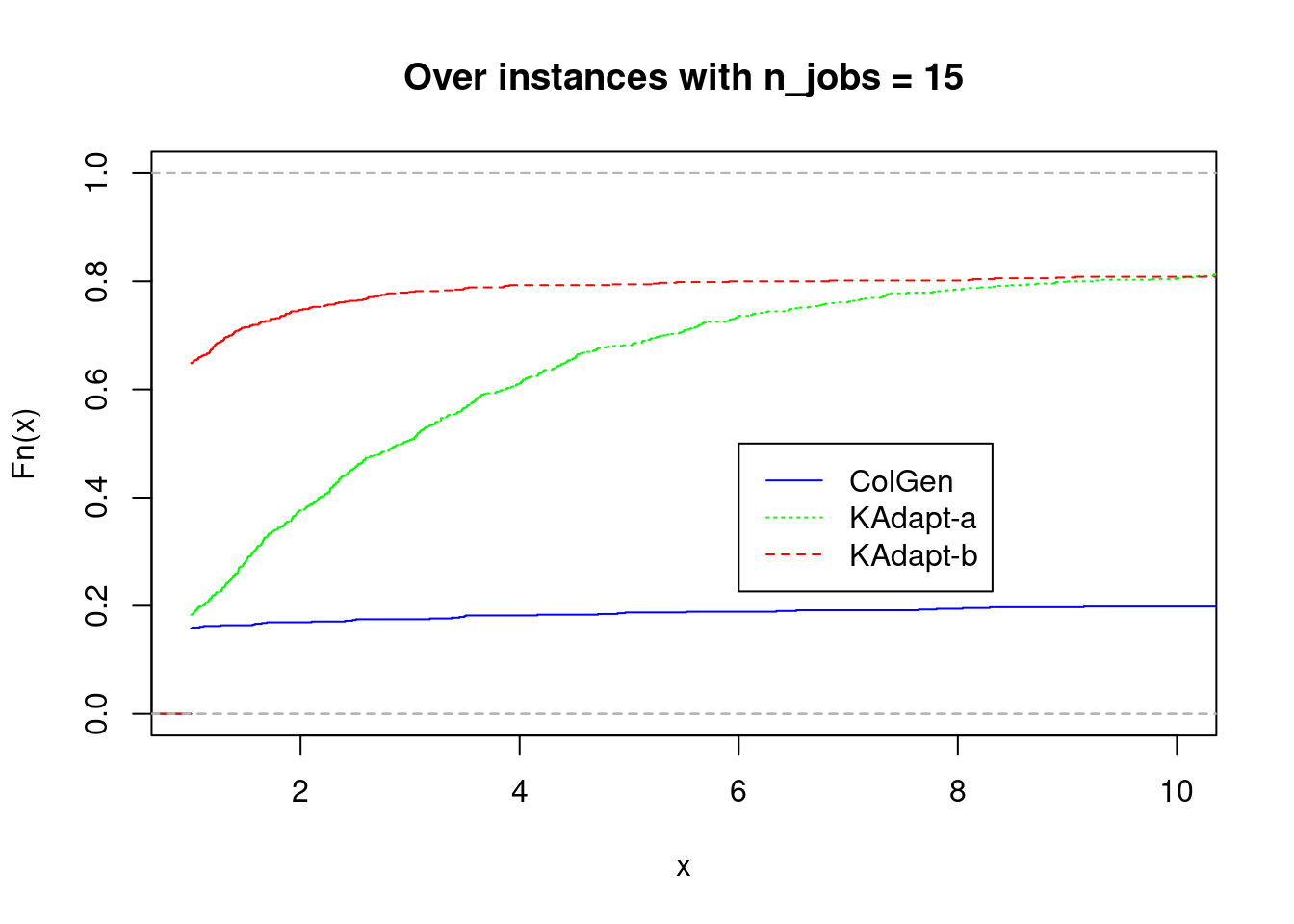
plot_performance_profile(fastest2[fastest2$n_jobs == 15,], title = "Over instances with n_jobs = 15")
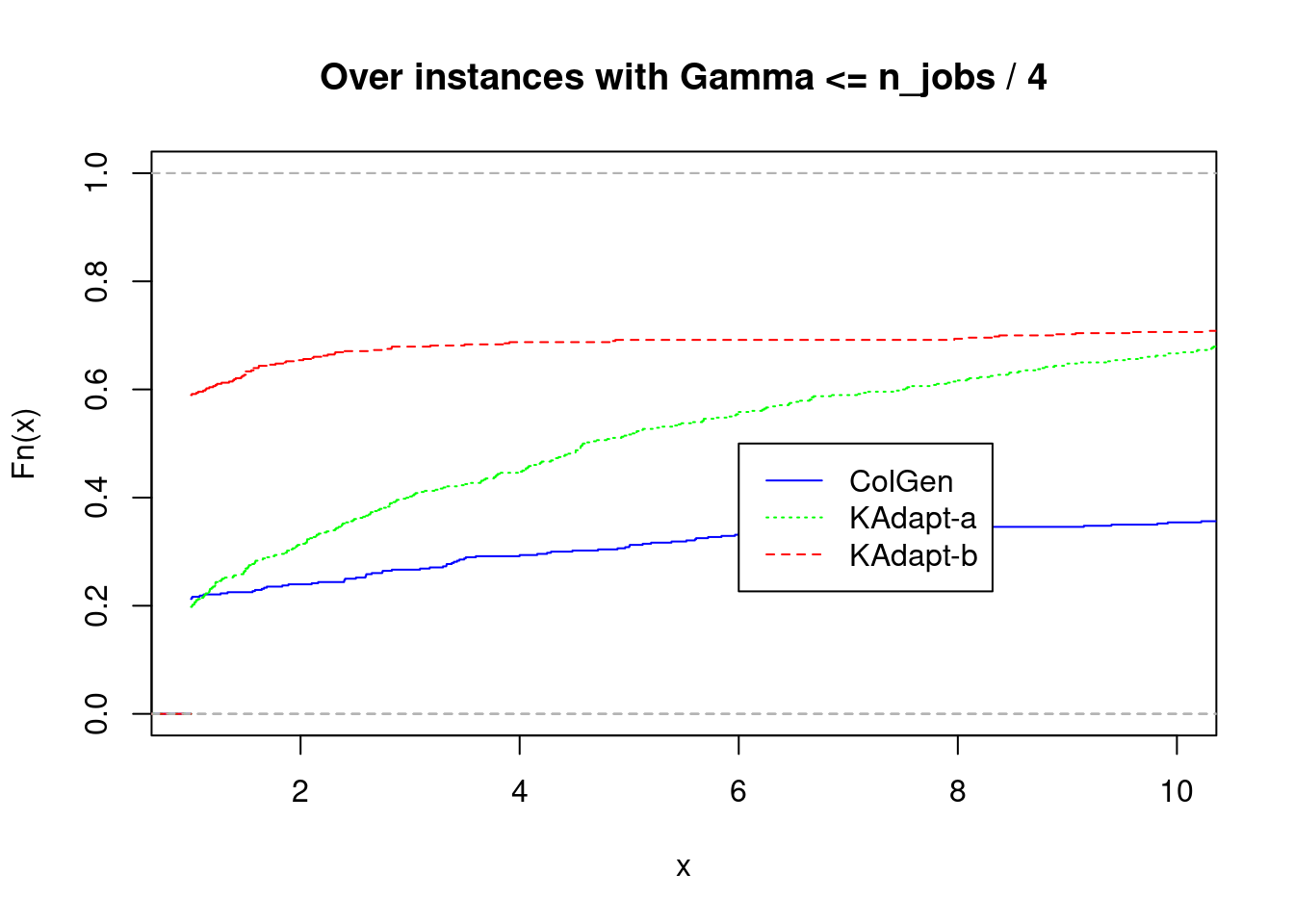
plot_performance_profile(fastest2[fastest2$gamma <= fastest2$n_jobs / 4,], title = "Over instances with Gamma <= n_jobs / 4")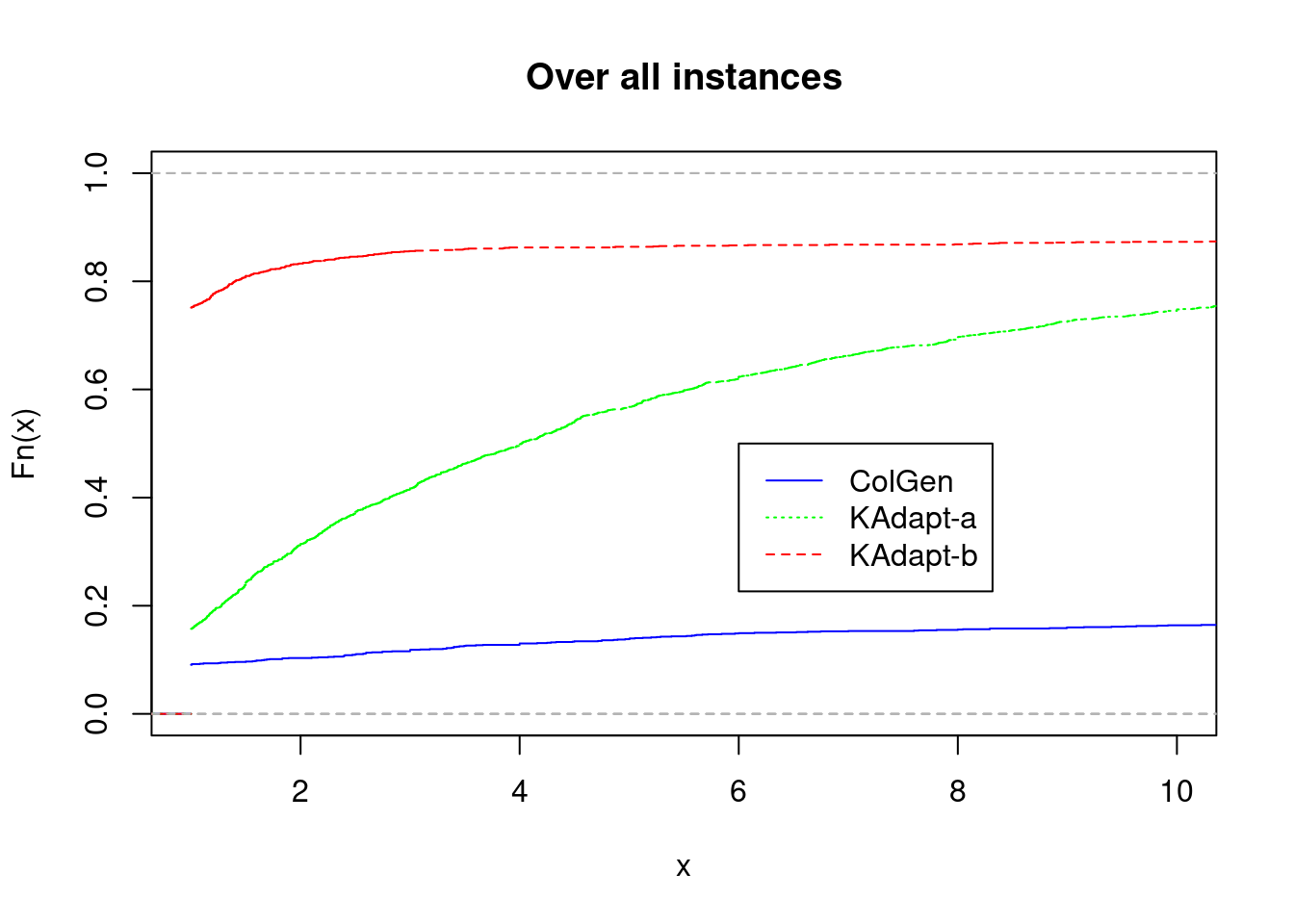
Feasible solutions found
compute_feasible_found_by_group = function(data, n_jobs) {
data = data[data$time >= 3600 & data$n_jobs == n_jobs,]
feasible_found = aggregate(is.finite(data$gap) & data$gap > 1e-4, by = list(data$gamma), sum)
colnames(feasible_found) = c("gamma", "feasible_found")
total = aggregate(data$instance, by = list(data$gamma), length)
colnames(total) = c("gamma", "total")
feasible_found$feasible_found = feasible_found$feasible_found / total$total * 100
return (feasible_found)
}feasible_found_colgen1 = compute_feasible_found_by_group(colgen1, 25)
feasible_found_kadapt1_a = compute_feasible_found_by_group(kadapt1_a, 25)
feasible_found_kadapt1_b = compute_feasible_found_by_group(kadapt1_b, 25)Table42 = cbind(
feasible_found_kadapt1_a,
feasible_found_kadapt1_b$feasible_found,
feasible_found_colgen1$feasible_found
)|
Feasible solutions found (%)
|
|||
|---|---|---|---|
| \(\Gamma\) | KAdapt1-a | KAdapt1-b | ColGen1 |
| 1 | 100 | 100 | 29 |
| 2 | 100 | 100 | 30 |
| 3 | 100 | 100 | 15 |
| 4 | 100 | 100 | 7 |
| 5 | 100 | 100 | 6 |
| 6 | 100 | 100 | 6 |
| 7 | 100 | 100 | 14 |
| 8 | 100 | 100 | 10 |
| 9 | 100 | 100 | 38 |
| 10 | 100 | 100 | 25 |
Approximation cost
compute_approximation_cost = function(colgen, k_adaptability, k_star) {
# Merge results from colgen with those obtained by K-adaptability
data = merge(colgen, k_adaptability, by = c("instance", "gamma"), all.y = TRUE)
data = data[,c("instance", "gamma", "time.x", "time.y", "objective.x", "objective.y", "k.y")]
colnames(data) = c("instance", "gamma", "time_colgen", "time_kadapt", "obj_colgen", "obj_kadapt", "k")
# Only consider those instances where both methods have converged
data = data[data$time_colgen < 3600 & data$time_kadapt < 3600,]
# Merge the resulting with the estimates of K^*
data = merge(data, k_star, by = c("instance", "gamma"), all.x = TRUE)
colnames(data)[7] = "k"
colnames(data)[8] = "k_star"
# Only consider those rows with K <= K^*
data = data[data$k <= data$k_star,]
# Compute approximation gap
data$approximation_cost = (data$obj_kadapt - data$obj_colgen) / data$obj_colgen * 100
# Compute time ratio
data$time_ratio = data$time_kadapt / data$time_colgen
return (data)
}approximation_costs1a = compute_approximation_cost(colgen1, kadapt1_a, k_star1_a)
approximation_costs2a = compute_approximation_cost(colgen2, kadapt2_a, k_star2_a)compute_approximation_cost_by_group = function(approximation_cost) {
# Compute mean of approximation_cost and time_ratio
result = aggregate(approximation_cost[,c("approximation_cost", "time_ratio")], by = list(approximation_cost$k_star, approximation_cost$k), mean)
colnames(result)[1:2] = c("k_star", "k")
# Count instances in each category
total = aggregate(approximation_cost$instance, by = list(approximation_cost$k_star, approximation_cost$k), length)
result$total = total[[3]]
result = result[order(result$k_star, result$k),]
rownames(result) = NULL
return (result)
}Table43 = compute_approximation_cost_by_group(approximation_costs1a)
Table45 = compute_approximation_cost_by_group(approximation_costs2a)For problem \(({\mathcal P})\)
| \(K^*\) | \(K\) | Approximation gap (%) | Time ratio | # Instances |
|---|---|---|---|---|
| 1 | 1 | 0.00 | 0.03 | 1989 |
| 2 | 1 | 6.69 | 0.00 | 587 |
| 2 | 2 | 0.00 | 5.23 | 110 |
| 3 | 1 | 5.86 | 0.01 | 368 |
| 3 | 2 | 1.43 | 6.00 | 368 |
| 3 | 3 | 0.00 | 14.59 | 90 |
| 4 | 1 | 6.30 | 0.01 | 123 |
| 4 | 2 | 2.06 | 0.09 | 123 |
| 4 | 3 | 0.60 | 14.23 | 123 |
| 4 | 4 | 0.00 | 13.27 | 32 |
| 5 | 1 | 6.85 | 0.01 | 16 |
| 5 | 2 | 2.25 | 0.04 | 16 |
| 5 | 3 | 0.67 | 0.82 | 16 |
| 5 | 4 | 0.24 | 34.76 | 16 |
| 5 | 5 | 0.00 | 29.28 | 3 |
| 6 | 1 | 1.92 | 0.01 | 3 |
| 6 | 2 | 1.70 | 0.02 | 3 |
| 6 | 3 | 0.58 | 0.05 | 3 |
| 6 | 4 | 0.13 | 0.31 | 3 |
| 6 | 5 | 0.02 | 5.87 | 3 |
| 6 | 6 | 0.00 | 2.06 | 2 |
For problem \((\widetilde{\mathcal P})\)
| \(K^*\) | \(K\) | Approximation gap (%) | Time ratio | # Instances |
|---|---|---|---|---|
| 1 | 1 | 0.00 | 0.23 | 1165 |
| 2 | 1 | 4.88 | 0.06 | 87 |
| 2 | 2 | 0.00 | 0.11 | 87 |
| 3 | 1 | 6.37 | 0.02 | 76 |
| 3 | 2 | 0.97 | 0.09 | 76 |
| 3 | 3 | 0.00 | 3.74 | 65 |
| 4 | 1 | 7.15 | 0.04 | 93 |
| 4 | 2 | 1.65 | 0.09 | 93 |
| 4 | 3 | 0.40 | 2.01 | 73 |
| 4 | 4 | 0.00 | 5.79 | 59 |
| 5 | 1 | 7.93 | 0.00 | 40 |
| 5 | 2 | 2.72 | 0.03 | 40 |
| 5 | 3 | 0.83 | 0.53 | 40 |
| 5 | 4 | 0.19 | 8.75 | 40 |
| 5 | 5 | 0.00 | 14.17 | 14 |
| 6 | 1 | 5.84 | 0.01 | 14 |
| 6 | 2 | 2.98 | 0.02 | 14 |
| 6 | 3 | 1.12 | 0.09 | 14 |
| 6 | 4 | 0.41 | 0.81 | 14 |
| 6 | 5 | 0.09 | 13.24 | 14 |
| 6 | 6 | 0.00 | 35.19 | 6 |
| 7 | 1 | 0.37 | 0.01 | 2 |
| 7 | 2 | 0.37 | 0.02 | 2 |
| 7 | 3 | 0.37 | 0.14 | 2 |
| 7 | 4 | 0.37 | 0.65 | 2 |
| 7 | 5 | 0.14 | 5.52 | 2 |
| 7 | 6 | 0.03 | 78.13 | 2 |
Fixed-order costs analysis
compute_fixed_order_costs = function(t_colgen1, t_colgen2) {
result = merge(t_colgen1, t_colgen2, by = c("instance", "gamma"))
result = result[,c("instance", "gamma", "n_jobs.x", "objective.x", "objective.y", "time.x", "time.y")]
colnames(result)[3:7] = c("n_jobs", "obj_colgen1", "obj_colgen2", "time_colgen1", "time_colgen2")
result = result[result$time_colgen1 < 3600 & result$time_colgen2 < 3600,]
result$gap = (result$obj_colgen2 - result$obj_colgen1) / result$obj_colgen1 * 100
return (result)
}fixed_order_costs = compute_fixed_order_costs(colgen1, colgen2)compute_fixed_order_costs_by_group = function(t_fixed_order_costs) {
result = aggregate(t_fixed_order_costs[,c("obj_colgen1", "obj_colgen2", "gap")], by = list(t_fixed_order_costs$n_jobs, t_fixed_order_costs$gamma), mean)
colnames(result)[1:2] = c("n_jobs", "gamma")
total = aggregate(t_fixed_order_costs$instance, by = list(t_fixed_order_costs$n_jobs, t_fixed_order_costs$gamma), length)
result$total = total[[3]]
result = result[order(result$n_jobs, result$gamma),]
rownames(result) = NULL
return (result)
}Table46 = compute_fixed_order_costs_by_group(fixed_order_costs)|
Objective cost
|
|||||
|---|---|---|---|---|---|
| \(&#124;\mathcal J&#124;\) | \(\Gamma\) | Free (ColGen1) | Fixed order (ColGen2) | Gap (%) | # Instances |
| 5 | 1 | 70.39 | 70.40 | 0.00 | 80 |
| 5 | 2 | 75.27 | 75.28 | 0.01 | 80 |
| 5 | 3 | 75.94 | 75.94 | 0.00 | 80 |
| 10 | 1 | 144.76 | 145.14 | 0.45 | 80 |
| 10 | 2 | 165.92 | 166.21 | 0.25 | 80 |
| 10 | 3 | 171.73 | 171.80 | 0.05 | 80 |
| 10 | 4 | 173.24 | 173.26 | 0.01 | 80 |
| 10 | 5 | 173.61 | 173.61 | 0.00 | 80 |
| 10 | 6 | 173.70 | 173.70 | 0.00 | 80 |
| 10 | 7 | 173.70 | 173.70 | 0.00 | 80 |
| 15 | 1 | 192.83 | 193.32 | 0.29 | 74 |
| 15 | 2 | 232.46 | 233.06 | 0.32 | 67 |
| 15 | 3 | 248.97 | 249.57 | 0.27 | 70 |
| 15 | 4 | 253.39 | 253.78 | 0.16 | 74 |
| 15 | 5 | 254.77 | 254.91 | 0.05 | 77 |
| 15 | 6 | 255.35 | 255.37 | 0.01 | 77 |
| 15 | 7 | 255.74 | 255.74 | 0.00 | 78 |
| 15 | 8 | 256.98 | 256.98 | 0.00 | 80 |
| 15 | 9 | 256.98 | 256.98 | 0.00 | 80 |
This document is automatically generated after every
git push action on the public repository
hlefebvr/hlefebvr.github.io using rmarkdown and Github
Actions. This ensures the reproducibility of our data manipulation. The
last compilation was performed on the 20/01/26 18:20:17.
 Henri Lefebvre
Henri Lefebvre